Rumus trigonometri merupakan bagian dari geometri. Sehingga untuk memahami geometri anda terlebih dahulu bisa memahami rumus trigonometri. Sejak berada di bangku sekolah menengah pertama tentunya anda sudah pernah berkenalan dengan rumus trigonometri, maka dari itu rumus-rumus di bawah ini bisa membantu anda untuk refresh kembali ingatan anda mengenai rumus trigonometri.
Terdapat banyak rumus trigonometri yang bisa anda pelajari di bawah ini, mulai dari rumus fungsi trigonometri, rumus setengah sudut trigonometri, rumus jumlah dan selisih sudut trigonometri, Rumus Perkalian Trigonometri, Rumus identitas trigonometri, rumus sudut rangkap dua dan sudut rangkap tiga trigonometri, dan rumus jumlah serta selisih trigonometri.
Daftar Isi
Rumus Trigonometri – Pengertian Trigonometri
Trigonometri atau kalau dilihat dari bahasa Yunani yaitu trigonon = “tiga sudut” dan metron = “mengukur” ialah sebuah cabang ilmu matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga. Dimana trigonometri ini muncul pada abad ke-3 SM (Sebelum Masehi) di masa hellenistikguna mempelajari tentang astronomi
Sebelum memasuki rumus trigonometri, maka ada baiknya anda mengetahui mengenai konsep dasar dari trigonometri matematika. Konsep trigonometri matematika adalah tentang kesebangunan segitiga siku-siku dan sisi-sisi yang bersesuaian pada dua bangun beserta bangun lain yang memiliki perbandingan yang sama. Konsep dasar trigonometri ini sangat lekat dengan tabel sin cos tan, maka mungkin ada baiknya anda memahami tabel tersebut juga.
Rumus Trigonometri – Fungsi Trigonometri
Fungsi trigonometri merupakan suatu fungsi yang grafik nya berulang secara terus menerus dalam periode tertentu. Fungsi dari periode itu sendiri merupakan suatu jarak antara dua puncak/lembah atau jarak antara awal puncak dan akhir lembah. Selain itu, terdapat amplitudo yang merupakan setengah dari selisih nilai maksimum dan minimum dari suatu fungsi. Rumus amplitudo sebagai berikut:
- 1 Rumus Amplitudo
- 2 Segitiga Siku-siku
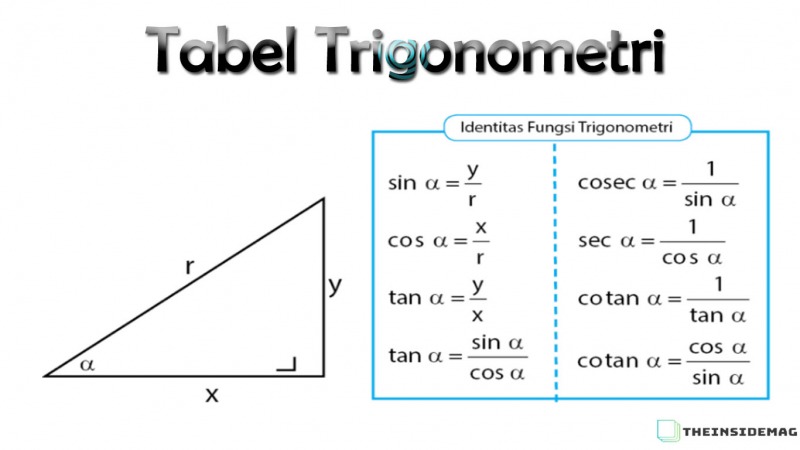
Perhatikan gambar segitiga siku-siku di atas. Di dalam rumus trigonometri terdapat tiga fungsi, fungsi pertama adalah sinus (sin) yang merupakan perbandingan sisi segitiga (pada segitiga siku-siku atau segitiga yang salah satu sisinya memiliki sudut 90°) yang berhadapan dengan sisi miring pada segitiga. Kemudian sisi kedua ialah cosinus (cos) yang merupakan perbandingan sisi segitiga yang terletak pada sisi miring. Fungsi yang terakhir ialah tangen (tan) yang merupakan perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut.
- 3 Rumus Fungsi Trigonometri
Rumus di atas merupakan rumus untuk mencari nilai masing-masing fungsi trigonometri.
Rumus Trigonometri – Rumus Setengah Sudut Trigonometri
Rumus trigonometri memiliki banyak variasi, diantaranya ialah rumus setengah sudut trigonometri atau sering disebut juga rumus trigonometri sudut pertengahan. Digunakan untuk menentukan nilai fungsi trigonometri sebuah sudut (bukan sudut yang istimewa) tanpa menggunakan kalkulator maupun alat bantu hitung lainnya. Contoh sudut istimewa yang dimaksud adalah 30°, 45°, 90°. Untuk sudut yang bukan sudut istimewa adalah 75°, 105°, 135°, dan lain sebagainya.
Berikut merupakan rumus setengah sudut trigonometri:
- 4 Rumus Setengah Sudut Trigonometri
Rumus Trigonometri – Rumus Jumlah Sudut Trigonometri
Untuk mencari nilai dari jumlah fungsi trigonometri, maka anda bisa menggunakan rumus di bawah ini. Rumus di bawah ini juga bisa anda gunakan untuk mencari selisih dari sudut trigonometri. Karena prinsipnya adalah penjumlahan dan pengurangan. Berikut rumus jumlah dan selisih sudut trigonometri:
- 5 Rumus jumlah dan selisih sudut trigonometri
Rumus Trigonometri – Rumus Perkalian Trigonometri Matematika
Dengan berbagai variasi rumus trigonometri yang ada, agar anda Selain untuk mencari nilai-nilai dari rumus di atas, trigonometri juga memiliki rumus yang berbeda untuk rumus perkalian trigonometri matematika. Agar anda bisa menemukan nilai dari sebuah soal perkalian, maka anda bisa menggunakan rumus di bawah ini:
- 6 Rumus Perkalian Trigonometri Matematika
Rumus trigonometri perkalian ini sangat praktis dan bisa digunakan untuk memecahkan berbagai persoalan. Kemudian rumus ini juga merupakan rumus yang seringkali menjadi rumus rujuan atau rumus yang diturunkan kemudian membentuk rumus lainnya.
Rumus Trigonometri – Rumus Identitas Trigonometri Matematika
Rumus identitas trigonometri merupakan rumus yang bisa menyatakan hubungan suatu fungsi dengan fungsi trigonometri lainnya. Misalkan saja, fungsi secan yang bisa saja merupakan fungsi kebalikan dari fungsi cos. Hal ini berlaku untuk fungsi kebalikan yang lain juga. Kemudian, selain mengetahui tentang fungsi kebalikan, rumus identitas trigonometri juga dapat menyatakan hubungan antar fungsi trigonometri.
Beberapa hubungan antar persamaan dapat dilihat melalui rumus berikut:
- 7 Rumus Identitas Trigonometri Matematika
Sesungguhnya, ada banyak sekali rumus fungsi identitas trigonometri. Akan tetapi fungsi identitas fungsi identitas trigonometri yang di atas hanyalah sebagian dan yang paling sering digunakan. Kemudian rumus tersebut merupakan rumus yang diturunkan dan diperoleh dari menghubungkan satu fungsi trigonometri dengan fungsi trigonometri lainnya.
Maka dari itu, kami sebut bahwa fungsi identitas memiliki banyak sekali rumus. Akan tetapi fungsi-fungsi di atas dapat dibuktikan kebenarannya. Cara membuktikan kebenaran rumus tersebut cukup mudah, yakni hanya dengan merubah ruas kiri agar bisa sama dengan ruas kanan maupun sebaliknya.
Rumus Trigonometri – Rumus Sudut Rangkap Dua Trigonometri
Rumus sudut Rangkap dua trigonometri merupakan rumus yang digunakan untuk mencari nilai besar sudut trigonometri di luar sudut istimewa. Misalnya, anda hanya mengetahui bahwa sudut 60O, namun sudut tersebut terlalu mudah diketahui karena sudut tersebut merupakan sudut yang istimewa, lantas bagaimana kah anda bisa mengetahui nilai dari sudut 120O? Padahal sudut tersebut bukan merupakan sudut istimewa.
Pada saat itulah rumus trigonometri sudut rangkap digunakan. Nilai dari sudut 120Otidak lain merupakan hasil dari 2 x 60O. Sehingga meskipun sudut 120Obukanlah sudut yang istimewa, namun sudut 60Omerupakan sudut yang istimewa dan dapat diketahui nilainya. Maka dari itu dengan memanfaatkan rumus trigonometri rangkap, besar nilai dari sudut 120Obisa anda ketahui dengan mudah tanpa memakai kalkulator.
Berikut merupakan uraian mengenai rumus sudut rangkap dua trigonometri. Dengan uraian di bawah diharapkan anda bisa lebih mengerti tentang sudut rangkap dua trigonometri.
GB 8. Rumus Sudut Rangkap Dua
Rumus Trigonometri – Rumus Sudut Rangkap Tiga Trigonometri
Memiliki konsep yang hampir sama dengan sudut rangkap dua trigonometri, pada rumus sudut rangkap tiga trigonometri juga digunakan untuk mencari besar nilai dari sudut yang di luar sudut istimewa. Misalnya anda hanya mengetahui bahwa sudut 45O, namun sudut tersebut terlalu mudah diketahui karena sudut tersebut merupakan sudut yang istimewa, lantas bagaimana kah anda bisa mengetahui nilai dari sudut 135 O? Padahal sudut tersebut bukan merupakan sudut istimewa.
Pada saat itulah rumus trigonometri sudut rangkap digunakan. Nilai dari sudut 135Otidak lain merupakan hasil dari 3 x 45O. Sehingga meskipun sudut 135Obukanlah sudut yang istimewa, namun sudut 45Omerupakan sudut yang istimewa dan dapat diketahui nilainya. Maka dari itu dengan memanfaatkan rumus trigonometri rangkap, besar nilai dari sudut 135Obisa anda ketahui dengan mudah tanpa memakai kalkulator.
Berikut merupakan uraian yang lebih jelas mengenai rumus trigonometri sudut rangkap tiga. Sehingga bisa anda pahami dan cermati lebih lanjut.
Rumus Trigonometri – Rumus Selisih Sudut Trigonometri
Untuk mencari nilai dari jumlah fungsi trigonometri, maka anda bisa menggunakan rumus di bawah ini. Rumus di bawah ini juga bisa anda gunakan untuk mencari selisih dari sudut trigonometri. Karena prinsipnya adalah penjumlahan dan pengurangan. Berikut rumus jumlah dan selisih sudut trigonometri:
- 9 Rumus jumlah dan selisih sudut trigonometri
Berikut merupakan contoh soal trigonometri yang bisa anda kerjakan guna mengaplikasikan rumus-rumus yang telah anda simak dan pelajari di atas. Kemudian pada bagian jawaban telah disediakan pembahasan yang mudah dimengerti sehingga anda bisa mencocokan dengan jawaban milik anda. Terdapat dua soal yang mudah, sehingga anda bisa memecahkannya tanpa kesulitan.
Kemudian agar anda semakin mengerti dengan perhitungan trigonometri sebaiknya anda mencari lebih banyak contoh soal yang memiliki cara pembahasan yang mudah. Selamat mencoba!
Contoh Soal Trigonometri
- Hitunglah nilai dari: 2 cos 75° cos 15°
Pembahasan :
Sebelum menjawab soal di atas, anda harus mengetahui fungsi trigonometri di atas merupakan fungsi apa? Sehingga anda bisa dengan mudah mengaplikasikan rumus yang telah di uraikan pada penjelasan sebelumnya.
Pada soal di atas kita bisa mengambil kesimpulan bahwa soal di atas merupakan contoh soal mengenai fungsi perkalian trigonometri. Sehingga kita bisa mencermati kembali rumus tentang perkalian trigonometri yang ada pada penjelasan sebelumnya.
Rumus perkalian trigonometri
2 cos A cos B = cos (A + B) + cos (A- B)
Jawaban :
nilai 2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
Maka nilai dari 2 cos 75° cos 15° yaitu ½
2.Temukanlah nilai dari sin 105° + sin 15°
Pembahasan :
Sebelum menjawab soal di atas, anda harus mengetahui fungsi trigonometri di atas merupakan fungsi apa? Sehingga anda bisa dengan mudah mengaplikasikan rumus yang telah di uraikan pada penjelasan sebelumnya.
Kemudian, pada soal di atas, kita bisa menarik kesimpulan jika contoh soal tersebut merupakan soal penjumlahan trigonometri. Sehingga kita bisa mencermati kembali rumus tentang penjumlahan trigonometri yang ada pada penjelasan sebelumnya.
Berikut merupakan rumus untuk memecahkan soal di atas:
2sin ½ (A+B) cos ½ (A-B)
Jawaban :
nilai sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
Maka nilai dari sin 105° + sin 15° adalah sin 60° cos 45°
Memahami soal matematika memang bukanlah hal yang mudah bagi beberapa orang, terlebih lagi mengenai rumus trigonometri. Namun dengan pembahasan di atas, kami berharap bahwa bisa membantu anda menyelesaikan persoalan trigonometri yang sedang anda coba pecahkan. Dengan demikian telah tiba pada akhir pembahasan kita mengenai rumus trigonometri matematika. Kami telah mengulas dengan lengkap disertai contoh soal dan pembahasan nya agar lebih mudah di pahami. Semoga uraian di atas bisa bermanfaat bagi pelajar tingkat Sekolah Menengah Atas dan siapapun yang membutuhkan. Selamat mencoba!
Rumus Trigonometri
Rumus trigonometri merupakan bagian dari geometri. Sehingga untuk memahami geometri anda terlebih dahulu bisa memahami rumus trigonometri. Sejak berad di bangku sekolah menengah pertama tentunya anda sudah pernah berkenalan dengan rumus trigonometri, maka dari itu rumus-rumus di bawah ini bisa membantu anda untuk merefresh kembali ingatan anda mengenai rumus trigonometri.
Terdapat banyak rumus trigonometri yang bisa anda pelajari di bawah ini, mulai dari rumus fungsi trigonometri, rumus setengah sudut trigonometri, rumus jumlah dan selisih sudut trigonometri, Rumus Perkalian Trigonometri, Rumus identitas trigonometri, rumus sudut rangkap dua dan sudut rangkap tiga trigonometri, dan rumus jumalah serta selisih trigonometri.
Rumus Trigonometri – Pengertian Trigonometri
Trigonometri atau kalau dilihat dari bahasa Yunani yaitu trigonon = “tiga sudut” dan metron = “mengukur” ialah sebuah cabang ilmu matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga. Dimana trigonometri ini muncul pada abad ke-3 SM (Sebelum Masehi) di masa hellenistikguna mempelajari tentang astronomi
Sebelum memasuki rumus trigonometri, maka ada baiknya anda mengetahui mengenai konsep dasar dari trigonometri matematika. Konsep trigonometri matemateika adalah tentang kesebangunan segitiga siku-siku dan sisi-sisi yang bersesuaian pada dua bangun beserta bangun lain yang memiliki perbandingan yang sama. Konsep dasar trigonometri ini sangat lekat dengan tabel sin cos tan, maka mungkin ada baiknya anda memahami tabel tersebut juga.
Rumus Trigonometri – Fungsi Trigonometri
Fungsi trigonometri merupakan suatu fungsi yang grafiknya berulang secara terus menerus dalam periode tertentu. Fungsi dari periode itu sendiri merupakan suatu jarak antara dua puncak/lembah atau jarak antara awal puncak dan akhir lembah. Selain itu, terdapat amplitudo yang merupakan setengah dari selisih nilai maksimum dan minimum dari suatu fungsi. Rumus amplitudo sebagai berikut:
- 1 Rumus Amplitudo
- 2 Segitiga Siku-siku
Perhatikan gambar segitiga siku-siku di atas. Di dalam rumus trigonometri terdapat tiga fungsi, fungsi pertama adalah sinus (sin) yang merupakan perbandingan sisi segitiga (pada segitiga siku-siku atau segitiga yang salah satu sisinya memiliki sudut 90°) yang berhadapan dengan sisi miring pada segitiga. Kemudian sisi kedua ialah cosinus (cos) yang merupakan perbandingan sisi segitiga yang terletak pada sisi miring. Fungsi yang terakhir ialah tangen (tan) yang merupakan perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut.
- 3 Rumus Fungsi Trigonometri
Rumus di atas merupakan rumus untuk mencari nilai masing-masing fungsi trigonometri.
Rumus Trigonometri – Rumus Setengah Sudut Trigonometri
Rumus trigonometri memiliki banyak variasi, diantaranya ialah rumus setengah sudut trigonometri atau sering disebut juga rumus trigonometri sudut pertengahan. Digunakan untuk menentukan nilai fungsi trigonometri sebuah sudut (bukan sudut yang istimewa) tanpa menggunakan kalkulator maupun alat bantu hitung lainnya. Contoh sudut istimewa yang dimaksud adalah 30°, 45°, 90°. Untuk sudut yang bukan sudut istimewa adalah 75°, 105°, 135°, dan lain sebagainya.
Berikut merupakan rumus setengah sudut trigonometri:
- 4 Rumus Setengah Sudut Trigonometri
Rumus Trigonometri – Rumus Jumlah Sudut Trigonometri
Untuk mencari nilai dari jumlah fungsi trigonometri, maka anda bisa menggunakan rumus di bawah ini. Rumus di bawah ini juga bisa anda gunakan untuk mencari selisih dari sudut trigonometri. Karena prinsipnya adalah penjumlahan dan pengurangan. Berikut rumus jumlah dan selisih sudut trigonometri:
- 5 Rumus jumlah dan selisih sudut trigonometri
Rumus Trigonometri – Rumus Perkalian Trigonometri Matematika
Dengan berbagai variasi rumus trigonometri yang ada, agar anda Selain untuk mencari nilai-nilai dari rumus di atas, trigonometri juga memiliki rumus yang berbeda untuk rumus perkalian trigonometri matematika. Agar anda bisa menemukan nilai dari sebuah soal perkalian, maka anda bisa menggunakan rumus di bawah ini:
- 6 Rumus Perkalian Trigonometri Matematika
Rumus trigonometri perkalian ini sangat praktis dan bisa digunakan untuk memecahkan berbagai persoalan. Kemudian rumus ini juga merupakan rumus yang seringkali menjadi rumus rujuan atau rumus yang diturunkan kemudian membentuk rumus lainnya.
Rumus Trigonometri – Rumus Identitas Trigonometri Matematika
Rumus identitas trigonometri merupakan rumus yang bisa menyatakan hubungan suatu fungsi dengan fungsi trigonometri lainnya. Misalkan saja, fungsi secan yang bisa saja merupakan fungsi kebalikan dari fungsi cos. Hal ini berlaku untuk fungsi kebalikan yang lain juga. Kemudian, selain mengetahui tentang fungsi kebalikan, rumus identitas trigonometri juga dapat menyatakan hubungan antar fungsi trigonometri.
Beberapa hubungan antar persamaan dapat dilihat melalui rumus berikut:
- 7 Rumus Identitas Trigonometri Matematika
Sesungguhnya, ada banyak sekali rumus fungsi identitas trigonometri. Akan tetapi fungsi identitas fungsi identitas trigonometri yang di atas hanyalah sebagian dan yang paling sering digunakan. Kemudian rumus tersebut merupakan rumus yang diturunkan dan diperoleh dari menghubungkan satu fungsi trigonometri dengan fungsi trigonometri lainnya.
Maka dari itu, kami sebut bahwa fungsi identitas memiliki banyak sekali rumus. Akan tetapi fungsi-fungsi di atas dapat dibuktikan kebenarannya. Cara membuktikan kebenaran rumus tersebut cukup mudah, yakni hanya dengan merubah ruas kiri agar bisa sama dengan ruas kanan maupun sebaliknya.
Rumus Trigonometri – Rumus Sudut Rangkap Dua Trigonometri
Rumus sudut Rangkap dua trigonometri merupakan rumus yang digunakan untuk mencari nilai besar sudut trigonometri di luar sudut istimewa. Misalnya, anda hanya mengetahui bahwa sudut 60O, namun sudut tersebut terlalu mudah diketahui karena sudut tersebut merupakan sudut yang istimewa, lantas bagaimana kah anda bisa mengetahui nilai dari sudut 120O? Padahal sudut tersebut bukan merupakan sudut istimewa.
Pada saat itulah rumus trigonometri sudut rangkap digunakan. Nilai dari sudut 120Otidak lain merupakan hasil dari 2 x 60O. Sehingga meskipun sudut 120Obukanlah sudut yang istimewa, namun sudut 60Omerupakan sudut yang istimewa dan dapat diketahui nilainya. Maka dari itu dengan memanfaatkan rumus trigonometri rangkap, besar nilai dari sudut 120Obisa anda ketahui dengan mudah tanpa memakai kalkulator.
Berikut merupakan uraian mengenai rumus sudut rangkap dua trigonometri. Dengan uraian di bawah diharapkan anda bisa lebih mengerti tentang sudut rangkap dua trigonometri.
GB 8. Rumus Sudut Rangkap Dua
Rumus Trigonometri – Rumus Sudut Rangkap Tiga Trigonometri
Memiliki konsep yang hampir sama dengan sudut rangkap dua trigonometri, pada rumus sudut rangkap tiga trigonometri juga digunakan untuk mencari besar nilai dari sudut yang di luar sudut istimewa. Misalnya anda hanya mengetahui bahwa sudut 45O, namun sudut tersebut terlalu mudah diketahui karena sudut tersebut merupakan sudut yang istimewa, lantas bagaimana kah anda bisa mengetahui nilai dari sudut 135 O? Padahal sudut tersebut bukan merupakan sudut istimewa.
Pada saat itulah rumus trigonometri sudut rangkap digunakan. Nilai dari sudut 135Otidak lain merupakan hasil dari 3 x 45O. Sehingga meskipun sudut 135Obukanlah sudut yang istimewa, namun sudut 45Omerupakan sudut yang istimewa dan dapat diketahui nilainya. Maka dari itu dengan memanfaatkan rumus trigonometri rangkap, besar nilai dari sudut 135Obisa anda ketahui dengan mudah tanpa memakai kalkulator.
Berikut merupakan uraian yang lebih jelas mengenai rumus trigonometri sudut rangkap tiga. Sehingga bisa anda pahami dan cermati lebih lanjut.
Rumus Trigonometri – Rumus Selisih Sudut Trigonometri
Untuk mencari nilai dari jumlah fungsi trigonometri, maka anda bisa menggunakan rumus di bawah ini. Rumus di bawah ini juga bisa anda gunakan untuk mencari selisih dari sudut trigonometri. Karena prinsipnya adalah penjumlahan dan pengurangan. Berikut rumus jumlah dan selisih sudut trigonometri:
- 9 Rumus jumlah dan selisih sudut trigonometri
Berikut merupakan contoh soal trigonometri yang bisa anda kerjakan guna mengaplikasikan rumus-rumus yang telah anda simak dan pelajari di atas. Kemudian pada bagian jawaban telah disediakan pembahasan yang mudah dimengerti sehingga anda bisa mencocokan dengan jawaban milik anda. Terdapat dua soal yang mudah, sehingga anda bisa memecahkannya tanpa kesulitan.
Kemudian agar anda semakin mengerti dengan perhitungan trigonometri sebaiknya anda mencari lebih banyak contoh soal yang memiliki cara pembahasan yang mudah. Selamat mencoba!
Contoh Soal Trigonometri
Hitunglah nilai dari: 2 cos 75° cos 15°
Pembahasan :
Sebelum menjawab soal di atas, anda harus mengetahui fungsi trigonometri di atas merupakan fungsi apa? Sehingga anda bisa dengan mudah mengaplikasikan rumus yang telah di uraikan pada penjelasan sebelumnya.
Pada soal di atas kita bisa mengambil kesimpulan bahwa soal di atas merupakan contoh soal mengenai fungsi perkalian trigonometri. Sehingga kita bisa mencermati kembali rumus tentang perkalian trigonometri yang ada pada penjelasan sebelumnya.
Rumus perkalian trigonometri
2 cos A cos B = cos (A + B) + cos (A- B)
Jawaban :
nilai 2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
Maka nilai dari 2 cos 75° cos 15° yaitu ½
Temukanlah nilai dari sin 105° + sin 15°
Pembahasan :
Sebelum menjawab soal di atas, anda harus mengetahui fungsi trigonometri di atas merupakan fungsi apa? Sehingga anda bisa dengan mudah mengaplikasikan rumus yang telah di uraikan pada penjelasan sebelumnya.
Kemudian, pada soal di atas, kita bisa menarik kesimpulan jika contoh soal tersebut meruapkan soal penjumlahan trigonometri. Sehingga kita bisa mencermati kembali rumus tentang penjumlahan trigonometri yang ada pada penjelasan sebelumnya.
Berikut merupakan rumus untuk memecahkan soal di atas:
2sin ½ (A+B) cos ½ (A-B)
Jawaban :
nilai sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
Maka nilai dari sin 105° + sin 15° adalah sin 60° cos 45°
Memahami soal matematika memang bukanlah hal yang mudah bagi beberapa orang, terlebih lagi mengenai rumus trigonometri. Namun dengan pembahasan di atas, kami berharap bahwa bisa membantu anda menyelesaikan persoalan trigonometri yang sedang anda coba pecahkan. Dengan demikian telah tiba pada akhir pembahasan kita mengenai rumus trigonometri matematika. Kami telah mengulas dengan lengkap disertai contoh soal dan pembahasannya agar lebih mudah di pahami. Semoga uraian di atas bisa bermanfaat bagi pelajar tingkat Sekolah Menengah Atas dan siapapun yang membutuhkan. Selamat mencoba!