Rumus pitagoras memang juga sering dikenal, dengan istilah teorema phytagoras atau pitagoras. Dalam hal ini, mungkin kalimat dari pitagoras sendiri sudah tidak asing lagi di telinga anda. Rumus ini memang sudah diajarkan sekolah dasar, lewat mata pelajaran matematika. Matematika juga sangat erat kaitannya dengan pitagoras sendiri. Rumus ini pertama kali, ditemukan oleh salah satu ilmuwan asal yunani bernama pitagoras.
Rumus dari pitagoras sendiri memiliki fungsi, dimana rumus ini digunakan untuk dapat mencari salah satu dari sisi dengan sisinya yang memang sudah di ketahui. Berikut ini adalah beberapa rumus dari pitagoras, yang dapat anda ingat dan memiliki fungsinya masing-masing.
Daftar Isi
Rumus pitagoras Segitiga Siku-siku
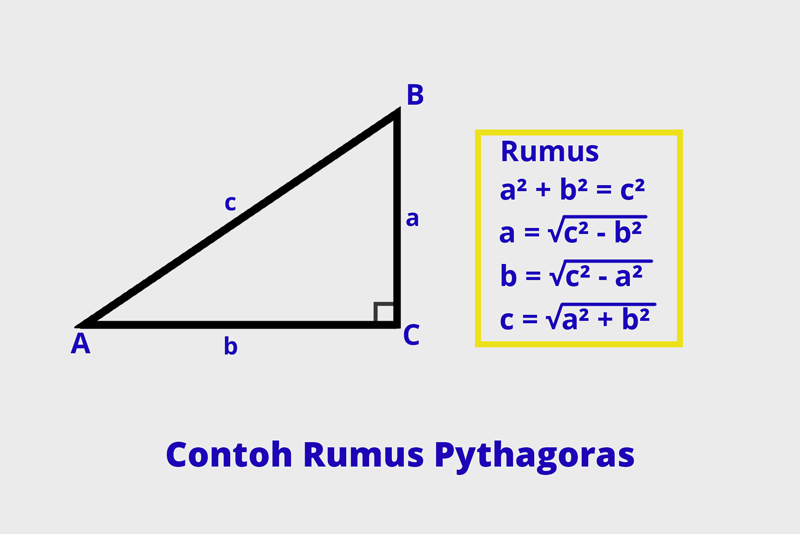
Segitiga siku-siku sendiri, adalah salah satu segitiga yang mana dibagi menjadi 3 bagian utama dalam tiap bagian yang dimilikinya. Dalam hal ini, segitiga siku-siku sendiri memiliki 2 sisi yang mana bagiannya saling tegak lurus. Selain itu, bagian kedua adalah memiliki 1 sisi miring dan bagian yang lainnya memiliki sudut yang berbentuk siku-siku.
Selain itu, bagian ketiga yang juga menjadi salah satu sifat, dari segitiga siku-siku ini adalah memiliki simetri lipat dan juga simetri putar. Berikut ini adalah rumus dari pitagoras segitiga siku-siku.
- Rumus untuk pitagoras sisi tegak dan juga sisi yang mendatar
B2 = a2 + c2
A2 = b2 – c2
C2 = b2 – a2
- Rumus untuk pitagoras yang dibuat, dalam bentuk akar. Rumus ini dapat anda gunakan, jika sisi miring yang dimilikinya adalah C dan juga sisi tegak dan mendatar yang dimiliki segitiga adalah a dan juga b.
a =
b =
c =
Rumus pitagoras Trapesium
Trapesium sendiri adalah sebuah bangun datar, yang mana memiliki bentuk dengan empat buah rusuk. Diantara rusuk yang dimilikinya, memiliki bentuk yang saling sejajar namun tidak memiliki panjang yang sama. Trapesium sendiri merupakan sebuah bangun datar, yang mana dapat anda hitung rumus dari pitagorasnya sendiri. Berikut ini adalah rumus pitagorastrapesium.
Rumus untuk menentukan pitagoras, dari tinggi trapesium adalah
Untuk anda yang ingin mengetahui bagaimana untuk menghitung sebuah rumus pitagoras yang diperuntukkan untuk trapesium, anda dapat melihat contoh soal berikut ini untuk mendapatkan penjelasan lebih lengkap.
Pada gambar trapesium diatas, telah diketahui bahwa panjang sisi PR adalah 40, panjang sisi RS adalah 40 dan juga sisi PQ adalah 64. Hitunglah luas yang dimiliki oleh trapesium ini, dengan menggunakan rumus pitagoras yang di tentukan.
Pembahasan:
Tentunya dalam hal ini, anda dapat melihat bahwa trapesium sendiri, merupakan bentuk dari trapesium sama kaki. Dengan begitu, anda dapat langsung menyimpulkan bahwa panjang yang dimiliki oleh QR sama dengan QS, panjang PT akan sama dengan UQ dan juga panjang RS akan sama dengan panjang TU, sehingga akan menciptakan rumus:
Panjang PT = PQ – TU – UQ
Panjang PT = 64 cm – 40 cm – UQ
Karena UQ = PT, maka:
2 x PT= 24 cm
Maka PT = 12 cm
Selanjutnya, anda dapat mencari tinggi dari trapesium. Dalam hal ini, anda dapat menggunakan rumus dari trapesium sebagai berikut:
RT =
RT=
RT=
RT=
RT= 38,15 cm.
Setelah sudah di dapatkan dari tinggi yang dimiliki oleh trapesium, anda dapat mencari luas yang dimiliki trapesium dengan rumus:
L = ½ x jumlah sisi sejajar x tinggi
L = ½ x (PQ + RS ) x RT
L = ½ x (64 cm + 40 cm) x 38,15 cm
L = ½ x 3967,6
L = 1983,8 cm2
Rumus pitagoras Kubus
Memang untuk menggunakan rumus seperti pitagoras, banyak juga digunakan untuk segitiga siku-siku. Namun selain segitiga siku-siku, rumus ini juga digunakan untuk menghitung bangun datar dan juga bangun dalam ruang matematika lainnya seperti kubus.
Anda dapat memperhatikan gambar diatas, dalam hal ini kubus memiliki sudut ABCD.EFGH. diagonal sisi yang dimiliki oleh kubus ini, merupakan salah satu ruas garis yang mana membantu untuk menghubungkan antara dua titi sudut yang dimiliki kubus yang mana berhadapan dengan bidang datar yang dimilikinya.
Diagonal yang dimiliki sisi kubus adalah ABCD.EFGH, yaitu AF, BD, CH, dan DE. Anda dapat memperhatikan bagaimana bentuk persegi yang dimiliki oleh ABCD, dimana pada sisi BD merupakan salah satu diagonal sisi yang memang dimiliki oleh ABCD. Setelah itu, anda dapat memperhatikan bentuk segitiga ABD, yang mana segitiga tersebut merupakan siku-siku yang dimiliki A.
Dalam hal ini, anda dapat menghitungnya dengan menggunakan teorema dari pitagoras sendiri.
BD² = AD² + AB²
BD² = a² + a²
BD² = 2a²
BD =
BD = a cm
Selanjutnya, anda dapat langsung menghitung berapa diagonal kubus dari ABCD.EFGH. diagonal ruang sendiri, merupakan salah satu diagonal yang mana menghubungkan antara dua titik yang berhadapan dalam suatu bangun ruang yang ada. Diagonal dari ruang kubus ini, merupakan BH dan juga FD. Anda dapat memperhatikan segitiga BDH sendiri.
Titik siku-siku pada kubus ini, memiliki bentuk segitiga yaitu titik D. maka dari itu, untuk menentukan panjang dari ruang HB sendiri, anda dapat mencarinya dengan menggunakan rumus dari pitagoras sebagai berikut:
HB² = BD² + DH²
HB² = (a√2)² + a²
HB² = 2a² + a²
HB² =3a²
HB =
HB = a cm
Rumus pitagoras Belah Ketupat
untuk dapat mengetahui bagaimana rumus untuk pitagoras pada belah ketupat, maka anda dapat memperhatikan bagaimana contoh soal yang akan diberikan.
Jika sudah diketahui sisi dari belah ketupat yang mana masing-masing memiliki 10 cm dan juga diagonal yang dimiliinya adalah 16 cm, maka anda dapat menghitung berapa luas yang dimiliki oleh belah ketupat diatas.
Penyelesaian:
Dapat dimisalkan bahwa titik perpotongan, yang dimiliki oleh diagonal AC dan juga BD maka di titik M dapat diketahui sebagai :
AM = ½ x AC
AM = ½ x 16 cm
AM = 8 cm
Jika dihitung menggunakan teorema atau rumus dari pitagoras sendiri, maka anda dapat mencari panjang yang dimiliki BM yaitu:
BM =
BM =
BM =
BM =
BM = 6 cm
Lalu dapat diketahui, bahwa:
BD = 2 x BM
BD = 2 x 6 cm
BD = 12 cm
Setelah sudah didapatkan sisi dari BD, maka anda dapat langsung mencari luas yang dimiliki oleh belah ketupat inim, yaitu:
L = ½ x d1 x d2
L = ½ x AC x BD
L = ½ x 16 cm x 12 cm
L = 96 cm2
Itulah luas bangun yang dimiliki oleh bangun belah ketipat ABCD diatas, dalam hal ini luasnya yaitu 96 cm2
Rumus pitagoras Jajargenjang
Untuk menggunakan rumus dari pitagoras sendiri, maka anda dapat memperhatikan bagaimana contoh soal yang akan diberikan berikut ini:
Anda dapat memperhatikan, berikut ini adalah bangun datar jajargenjang yang dimiliki oleh ABCD.
Dalam hal ini, diketahui bahwa panjang yang dimiliki oleh sisi AD adalah 13 cm, CD adalah 20 cm dan juga BE yang memiliki panjang 15 cm. Hitunglah berapa luas yang dimiliki, oleh luas dari jajargenjang tersebut:
Penyelesaian:
Langkah pertama yang dapat anda lakukan, cobalah untuk menggunakan sifat-sifat yang dimiliki jajargenjang, untuk dapat mencari panjang AE.
AB = CD
AE + BE = CD
AE = CD – BE
AE = 20 cm – 15 cm
AE = 5 cm
Lalu selanjutnya setelah mengetahui panjang dari AE, maka anda dapat mencari tinggi dari jajar genjang. Untuk menghitung tinggi yang dimiliki oleh jajargenjang ini dapat menggunakan rumus untuk pitagoras sendiri.
DE =
DE =
DE =
DE =
DE = 12 cm
Setelah dapat ditemukan, berapa sisi dari DE sendiri maka anda dapat mencari luas yang dimiliki oleh jajargenjang dengan menggunakan rumus dari pitagoras. Berikut adalah penyelesaiannya:
L = a x t
L = AB x DE
L = 20 cm x 12 cm
L = 240 cm2
Dengan perhitungan yang telah dilakukan, maka dapat diketahui bahwa luas yang dimiliki olej jajargenjang ini adalah 240 cm2.
Rumus pitagoras Limas
untuk anda yang ingin menghitung limas segitiga sendiri, anda dapat menggunakan rumus:
- Rumus yang digunakan, untuk anda yang ingin mencari luas alas dari limas yaitu ½ x a x t
- Rumus yang digunakan, unuk anda yang ingin mencari permukaan dari luas limas yaitu alas + jumlah seluruh sisi tegak yang dimiliki limas
- Rumus yang digunakan, untuk anda yang ingin mencari volume limas segitiga yaitu V = 1/3 x (1/2 x panjang x lebar ) x tinggi.
Berikut ini adalah contoh soal, dimana anda dapat lebih mengetahui bagaimana mengitung limas menggunakan rumus dari pitagoras sendiri. Terdapat sebuah alas dari limas, yang mana memiliki bentuk segitiga sama kaki. Limas tersebut memiliki panjang sisi alasnya 16 dm dan juga panjang kaki 10 cm. Hitunglah berapa volume, yang dimiliki limas jika tingginya 9 cm.
Penyelesaian:
Perlu anda perhatikan, bahwa alas yang dimiliki limas tersebut memiliki bentuk segitiga sama kaki. Jika anda dapat menggambarkannya, maka akan terjadi bentuk seperti berikut ini:
Untuk dapat mengetahui tinggi dari luas segitiga diatas, anda dapat menggunakan rumus dari pitagoras yaitu:
t² = 10² – 8²
t² = 100 – 64
t² = 36
t = = 6
lalu setelah diketahui tinggi dari segitiga, anda dapat mencari luas yang dimiliki segitiga dengan rumus:
LΔ = ½ × a × t
LΔ = ½ × 16 × 6
LΔ = 48 cm²
Lalu dapat disimpulkan, bahwa volume limas secara keseluruhan adalah:
L = 1/3 × luas alas × tinggi
L = 1/3 × 48 cm² × 9 cm
L = 144 cm²
Rumus pitagoras Persegi
Untuk mencari rumus dari pitagoras yang diperuntukkan untuk persegi, dalam hal ini jumlah yang dimiliki oleh luas persegi pada kaki segitiga sama dengan luas yang dimiliki persegi pada sisi miring yang dimiliki oleh segitiga. Berikut ini adalah contoh soal, dimana anda dapat menggunakan rumus dari pitagoras sendiri.
L1 + L2 = L3
( a x a ) + ( b x b ) = ( c x c )
a2 + b2 = c2
setelah itu, nantinya dapat diperoleh :
a =
b =
c =
Masih banyak lagi rumus-rumus dari pitagoras yang dapat anda kuasai dan pelajari. Rumus menggunakan pitagoras tersebut dapat dikatakan mudah, jika anda sudah mengetahui panjang, luas, tinggi dari masing-masing bangun.