Rumus Tabung , Menghitung ukuran tabung bukanlah hal yang sulit ketika anda mengetahui rumus tabungyang harus digunakan. Sejak duduk di bangku sekolah dasar, kita telah mempelajari hal tersebut. Maka tentunya mencari volume, luas, hingga keliling tabung bukanlah hal yang sulit bagi kita semua.
Seiring berjalannya waktu, mungkin kita telah lupa bagaimana cara menghitung ukuran tabung yang benar dan mudah. Maka dari itu anda bisa menyimak ulasan berikut ini untuk mengetahui rumus tabung yang digunakan. Anda bisa mengukur luas, keliling hingga volume tabung dengan mudah dengan rumus-rumus yang ada di bawah ini.
Daftar Isi
Rumus Tabung – Menghitung Luas Alas
Untuk menghitung volume, keliling, maupun luas maka ada hal paling penting yang harus anda ketahui terlebih dahulu, yakni menghitung bagian alas dari tabung tersebut. Bagian dari alas tabung tersebut akan berbentuk lingkaran, maka dari itu kita bisa memasukkan rumus hitung lingkaran agar bisa menghitungnya dengan mudah.
Pertama perhatikan gambar di bawah ini, ini adalah rumus dari lingkaran.
Rumus bagian Lingkaran
Rumus Lingkaran :
| Perhitungan | Rumus | Satuan |
| Luas Lingkaran | L = π × d²/4 = π × r² | m2 |
| Keliling Lingkaran | K = π × d = 2 × π × r | m |
| Diameter Lingkaran | d = 2 × r | m |
Setelah memperhatikan gambar dan tabel di atas tentunya anda sudah memiliki gambaran tertentu mengenai rumus alas tabung atau lingkaran yang akan kita gunakan. Maka agar anda lebih mudah lagi untuk memahami bagaimana cara menghitung nya, kamu akan membantu untuk mengulas secara rinci satu persatu rumus alas tabung atau lingkaran (luas, keliling, diameter) disertai dengan contoh soal dan pembahasan nya.
Rumus Luas Lingkaran :
Luas Lingkaran = π x r²
Keterangan:
π ( phi ) = 3,14 atau 22/7
r = jari-jari dari lingkaran atau setengah diameter lingkaran, jika jari-jari satuan nya meter (m), maka satuan luasnya m².
Contoh Soal Menghitung Luas Lingkaran :
- Diketahui keliling bangun lingkaran ialah 88 cm dan nilai π adalah ²²⁄₇. Hitunglah luas lingkaran tersebut!
Jawab:
Karena untuk menghitung luas lingkaran menggunakan rumus π x r², kita cari terlebih dahulu nilai rnya.
Keliling = 2.π.r
88 = 2.π.r
Balikan
r = 88
2.π
r = 88
2.(²²/7)
r = 88 x 7
44
r = 2 x 7
r = 14 cm
Setelah menemukan nilai jari-jari(r) selanjutnya kita hitung luasnya.
L = π x r²
L = ²²⁄₇ x 14²
L = ²²⁄₇ x 14 x 14
L = 616 cm²
- Sebuah mobil memiliki velg dengan diameter 42 cm. Tentukan luas lingkaran velg mobil tersebut!
Jawab:
d = 42 cm
karena d = 2 kali r maka:
r = d/2
r = 42/2
r = 21 cm
Luas = π x r²
Luas =Rumus Lingkaran :
| Perhitungan | Rumus | Satuan |
| Luas Lingkaran | L = π × d²/4 = π × r² | m2 |
| Keliling Lingkaran | K = π × d = 2 × π × r | m |
| Diameter Lingkaran | d = 2 × r | m |
Rumus Tabung – Menghitung Keliling Lingkaran :
Keliling Lingkaran = π x d
karena d = 2 x r , bisa juga menggunakan rumus dibawah ini
Keliling lingkaran = π x 2 x r
Keterangan:
d merupakan diameter
r merupakan jari-jari
π = 22/7 atau 3.14
Nilai π = 22/7 jika jari-jari(r) atau diameter(d) merupakan kelipatan dari 7 atau bisa dibagi 7
Nilai π = 3,14 jika jari-jari(r) atau diameter(d) bukan kelipatan dari 7 atau tidak bisa dibagi 7
Contoh Soal Menghitung Keliling Lingkaran :
- hitunglah keliling lingkaran yang mempunyai jari-jari 10 cm. Jawab: r = 10 cm Π = 3,14 Keliling = 2 x π x r Keliling = 2 x 3,14 x 10 Keliling = 62,8 cm
- hitunglah keliling lingkaran yang memiliki diameter 20 cm! Jawab: d = 20 cm Π = 3,14 Keliling = π x d Keliling = 3,14 x 20 Keliling = 62,8 cm
Rumus Lingkaran :
| Perhitungan | Rumus | Satuan |
| Luas Lingkaran | L = π × d²/4 = π × r² | m2 |
| Keliling Lingkaran | K = π × d = 2 × π × r | m |
| Diameter Lingkaran | d = 2 × r | m |
Setelah memahami tentang alas tabung, yakni lingkaran tentunya anda akan lebih mudah memahami rumus-rumus di bawah ini. sebelum membawa anda lebih jauh untuk memahami rumus tabung. Ada baiknya kita mengetahui tentang seluk beluk tabung terlebih dahulu. Berikut penjelasannya:
Rumus Tabung – Pengertian Bangun Tabung
Pengertian Bangun Tabung
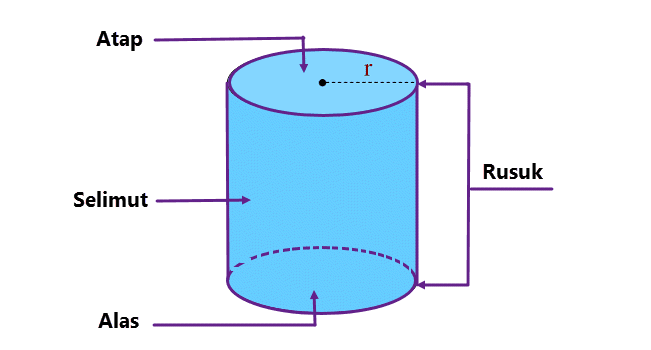
Tabung merupakan bagian dari Bangun ruang tiga dimensi. Bangun ruang tiga dimensi terbentuk dari tutup, alas, dan bagian selimut. Pada bagian tutup dan alas dari tabung merupakan sebuah lingkaran yang memiliki bentuk simetris atau sama besar. Kemudian pada bagian selimut merupakan persegi panjang yang menyelimuti tabung tersebut. Berikut gambar untuk memudahkan anda memahami.
Perhatikan Gambar berikut:
Gambar Contoh Tabung
Setelah mencermati gambar tabung yang ada di atas. Tentunya anda bisa menarik beberapa kesimpulan agar memudahkan anda menghitung rumus tabung.
- Tabung hanya memiliki dua buah rusuk saja.
- Tabung memiliki alas dan tutup yang terbentuk dari dua lingkaran yang masing-masing memiliki ukuran yang sama.
- Tabung terbagi menjadi tiga bagian, yakni pada bagian alas dan tutup yang berbentuk lingkaran. Kemudian, pada bagian selimut yang berbentuk persegi panjang.
Demikian adalah ciri-ciri dari tabung
Setelah beberapa pembahasan di atas tentunya anda semakin mengerti mengenai seluk-beluk tabung, anda sudah mengetahui cara menghitung dua bagian tabung, yakni pada bagian alas dan tutup. Maka berikut anda bisa langsung lanjut untuk mengetahui cara menghitung luas hingga volume tabung.
Rumus Tabung– Menghitung Luas Permukaan
Untuk memulai menghitung rumus luas permukaan tabung, maka pertama kita akan membahas mengenai jaring-jaring tabung. Jaring-jaring tabung terdiri dari:
- Tutup dan alas tabung yang membentuk bentuk lingkaran dengan besaran jari-jari (r), sehingga memiliki rumus luas lingkaran = 2πr². Kemudian untuk bagian jari-jarinya kita akan menggunakan rumus π= 22/7 atau 3,14.
- Pada bagian selimutnya atau bagian lengkungan nya, memiliki bentuk persegi panjang. Maka kita akan menggunakan rumus persegi panjang yakni P (keliling alas) x L (Tinggi tabung)
Maka rumus luas permukaan tabung yang didapatkan adalah sebagai berikut
Luas tutup serta alas tabung nya yaitu πr² + πr² = 2πr²
Luas selimut tabung yaitu: p (keliling alas) x l (tinggi tabung)
= 2πr x t
= 2πrtMaka, Luas permukaan tabung yaitu = Luas tutup + alas + selimut tabung = 2πr²+2πrt = 2πr(r+t)
Rumus Tabung – Menghitung Volume
Setelah anda memahami cara menghitung luas alas dan tutup, keliling alas dan tutup, hingga luas permukaan tabung. Tentunya ada akan semakin mudah untuk menghitung volume dari sebuah tabung.
Jika anda bingung apa itu yang disebut volume, maka kami akan memberi penjelasan singkat disini. Volume adalah ruang yang berada di dalam sebuah bangun, sehingga kita bisa mengetahui seberapa penuh tabung tersebut bisa diisi.
Selanjutnya, untuk mengetahui rumus volume sebenarnya cukup mudah. Hal ini hanyalah perkalian antara tinggi tabung dengan luas alas tabung. Dengan mengkalikan hal-hal yang dibutuhkan, maka anda bisa mengetahui volume tabung secara pasti.
Berikut merupakan pembahasan tentang rumus volume tabung disertai dengan contoh soal:
Volume Tabung = πr²t
Rumus Keliling Alas
Rumus nya yaitu:
Keliling alas = 2πr
Contoh Soal Tabung
Contoh Soal 1:
Hitunglah berapa volume tabung yang punya diameter 50 cm dan tinggi 66 cm?
Jawab :
diameter = 50 cm, karena r = 1/2 diameter maka r = 25 cm
tinggi = 66 cm
Rumus:
Volume Tabung = π x r² x t
= (22/7) x 25 cm² x 66 cm
= (22/7) x 25 x 25 x 66
= (22/7) x 41250
= 129.642 cm³.
Contoh Soal 2:
Seorang pemilik kebun, memotong sebuah pohon yang menjadi tabung atau silinder yang memiliki luas penampang dengan alasnya ialah 350 cm². Kayu tersebut memiliki tinggi 45 cm. Maka hitunglah volume tabung atau silinder dari kayu tersebut!
Jawab :
Volume silinder = luas penampang alas atau lingkaran x tinggi
Volume silinder kayu = 350 cm² x 45 cm = 15.750 cm³.
Maka, volume silinder tersebut ialah 15.750 cm³.
Contoh soal 3:
Sebuah kaleng memiliki diameter dan tinggi masing-masing 16 cm dan 12 cm. Berapa luas permukaan dari kaleng tersebut?
Jawab : 2 × phi × r (r+t)
2 × 22/7 × 8 (8 + 12)
44 (17) = 160
Luas selimut Tabung, rumus nya: 2 × phi × r × t
Contoh soalnya : Apabila diketahui sebuah tabung yang memiliki r = 14 dan tinggi 30. Tentukanlah luas selimut tabung tersebut:
Jawab :
Rumus: 2 × phi × r × t
2 × 22/7 × 14 × 30
44 × 50 = 2540
Sekarang cara mencari keliling alas suatu tabung.
Contoh soal:
Apabila ada sebuah tabung yang diketahui memiliki jari – jari yaitu 16 cm. Carilah dan hitinglah keliling alas tabung tersebut:
Penyelesaian :
Diketahui :
r = 16 cm
Yang ditanya : K = …?
Jawab :
K = 2 x π x r
K = 2 x 22/7 x 16
K = 704 / 7
K = 100.57 cm
Maka, keliling alas tabung tersebut ialah = 100.57 cm
Demikian adalah rumus tabung yang bisa anda gunakan dan aplikasikan dengan mudah. Agar lebih memahaminya anda bisa mencari contoh-contoh soal dan menerapkan rumus-rumus tabung yang sudah dijelaskan di atas. Dengan memahami rumus langkah demi langkah, maka dapat memudahkan anda untuk mengetahui seluk beluk dari tabung dengan mudah. Maka dari itu semoga rumus tabung yang kami berikan dapat bermanfaat bagi anda. Selamat mencoba!